Table of contents
들어가며
넥슨은 다양한 데이터와 지표들을 바탕으로 게임의 현재를 분석하고 미래를 그리고 있습니다.
오랫동안 유저와 함께하는 서비스를 만들려면 어떤 지표를 봐야할까요?
바로 오늘 소개드릴 LTV (LifeTime Value)가 해답이 될 수 있습니다.
LTV는 현재의 유저들의 미래 가치를 예측하여 중장기적인 성과를 측정하기 위해 개발한 지표입니다.
이번 포스트에서는 LTV가 어떻게 산출되고, 어떤 방식으로 모델링 되는지 자세히 살펴보도록 하겠습니다. 
LTV (LifeTime Value)
"고객 생애 가치"라 불리는 LTV는 유저의 향후 구매 금액을 나타내는 지표입니다. LTV를 활용하면 고객 유치 비용 대비 LTV가 높은지 판단해 마케팅이나 서비스 운영에서 장기적인 매출 성과를 측정할 수 있기 때문에 롱런하는 서비스를 만들 때 참고할 수 있는 지표이죠.
구체적으로 어떻게 LTV를 추정할까요?
LTV는 유저의 과거 구매 정보를 가지고 기대 구매 횟수와 기대 구매 금액을 예측해 이 둘의 곱으로 산출되는 지표입니다.
그림 1. LTV 산출 방식
유저 김넥슨의 LTV를 구하기 위해 필요한 데이터는 다음과 같습니다.
•
첫 구매 ~ 집계일까지의 기간 (Time):
•
첫 구매 ~ 마지막 구매까지의 기간 (Recency):
•
첫 구매 ~ 집계일까지의 구매 일수 (Frequency):
•
평균 구매 금액 (Monetary Value):
만약 3년 전부터 어제까지 주 5일씩 꾸준히 10만 원씩 구매하는 유저가 있다면 LTV는 얼마일까요?
단순 계산하면 주 5일 = 연 260일 정도 구매한 유저이기 때문에 260일 * 10만 원, 즉 1년에 2,600만 원 정도 소비할 것으로 예상할 수 있습니다. 그러나, 유저의 LTV는 이보다 적은 수치가 계산됩니다.
•
유저가 꾸준히 구매했더라도 어느 시점 이후 구매를 안 할 것이다 가정하기 때문에 기대 구매 일수를 260일보다 더 적게 예상하게 됩니다.
•
어제까지도 구매를 했으므로 이후에도 구매 금액이 비슷할 것이라 보아 기대 구매 금액을 10만 원 정도로 예상하게 됩니다.
이처럼, 기대 구매 일수와 기대 구매 금액을 예측하는 것이 LTV의 핵심인데요.
기대 구매 일수는 BG/NBD (Beta-Geometric / Negative Binoimal Distribution)라는 모델로, 기대 구매 금액은 Gamma-Gamma 모델로 추정이 됩니다. BG/NBD는 베타 분포와 기하 분포의 결합과 음이항 분포로 구성되고, Gamma-Gamma는 두 감마 분포의 결합으로 이루어집니다.
BG/NBD = BTYD (Buy Till You Die) 모델
BG/NBD 모델은 BTYD (Buy Till You Die) 모형이라고도 불리는데요. 구매 횟수에 대한 "Buy"에 대한 모형과 어느 시점 이후 구매를 하지 않을 확률 "Till You Die"에 대한 모형으로 나뉩니다.
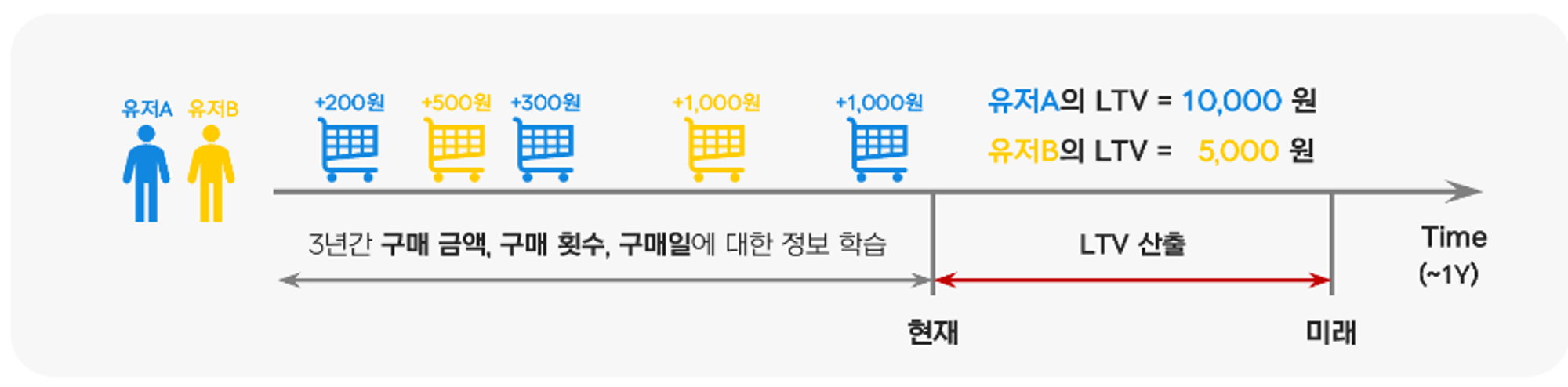
그림 2. LTV 산출 방식 (금액은 예시를 위해 만든 값)
위 그림은 유저 A와 B의 LTV를 산출하는 방식을 보여줍니다.
유저 A와 B는 3년 동안 총 1,500원을 소비했는데요. 이때 유저 A와 B 중 누가 더 LTV가 높을까요? 
직관적으로 생각했을 때 유저 A가 더 최근에 구매했고 구매 횟수도 많기 때문에 유저 A의 LTV가 더 높게 산출될 것입니다. 이처럼 유저의 ① 구매 횟수와 ② 다음에도 구매를 중단하지 않고 구매를 할 가능성을 따져 유저의 LTV를 산출하게 됩니다.
더 상세한 로직이 궁금하시다고요? 구체적으로 아래와 같이 확률 모형을 가정합니다.
1. Buy
“미래에 유저가 몇 번 구매할까?”에 대한 모델
Buy에 대한 답은 음이항 분포 (NBD, Negative Binomial Distribution)을 통해 추정할 수 있습니다.
유저가 남아있는 동안, 유저의 구매 횟수는 일정한 기간 동안의 구매율을 모수로 하는 포아송 분포를 따릅니다. 사실 포아송 분포는 "구매 횟수"에 대한 분포라 구매율을 모수로 하지 않고, 정해진 시간 동안의 예상 구매 횟수를 모수로 하는데요.
원 논문에서는 포아송 분포의 모수를 구매 횟수가 아닌 구매율 (transaction rate)로 표현하는데요. 아마도 일정한 기간을 어떻게 정의하느냐에 따라서 충분히 비율로 표현할 수 있기 때문이라 생각이 듭니다.
예를 들어, 1년에 30번 구매한 고객이 있다면 구매 횟수가 을 따른다고 말할 수도 있겠지만, 단위 기간을 이보다 더 좁은 기간인 1일로 정의한다면 1일에 의 확률로 구매를 한다 말할 수 있기 때문에 라고 말할 수 있는 것이죠.
유저마다 구매 횟수는 다르기 때문에 이 횟수에 대해 를 따른다고 가정합니다.
2. Till You Die
“미래에 유저가 언제 구매를 중단할까?”에 대한 모델
Till You Die에 대한 답은 베타 분포와 기하 분포 (BG, Beta Geometric) 을 통해 추정할 수 있습니다.
유저마다 구매를 더 이상 안 하게 되는 시점이 있다고 가정합니다. 따라서 마지막 구매 이후 더 이상 돌아 오질 않을 확률 (dropout rate)이 기하 분포 를 따른다 가정합니다.
이 확률 또한 유저마다 다르다고 가정해 를 따른다 가정합니다. 보통 베타 분포는 범위가 (0, 1)로 한정하기 때문에 확률에 대한 분포로 가정하기 좋습니다.
3. 알아두면 좋은 확률 지식
Buy와 Till You Die에 대해 확률 분포를 가정하는 것까지는 알겠는데, 여기서 몇 가지 의문점이 생기지 않으신가요?
NBD (Negative Binomial Distribution) 부분은 어디 갔을까? 
모형 이름이 BG/NBD인데 B에 해당하는 베타 분포 (Beta Distribution), G에 해당하는 기하 분포 (Geometric Distribution)은 있는 반면 NBD에 해당하는 음이항 분포 (Negative Binomial Distribution)는 어디서도 찾아볼 수 없는 것이 이상했습니다.
결론부터 말하면 포아송 분포와 감마 분포의 결합이 바로 음이항 분포에 해당합니다. 이를 Poisson-Gamma Mixture라 부릅니다.
대학교 때 여러 확률 분포를 배우는데 이들의 상생 관계를 이해하면 더 깊게 분포를 이해하실 수 있습니다.
예를 들어
•
베르누이 분포가 한 번 시행했을 때의 성공 횟수에 대한 분포라면, 베르누이 분포의 합은 이항 분포로, n번 시행했을 때의 성공 횟수에 대한 분포이며,
•
지수 분포가 사건이 1회 발생할 때까지의 대기 시간에 대한 분포라면, 지수 분포의 합은 감마 분포로, 사건이 n번 시행했을 때까지의 대기 시간에 대한 분포이며,
•
기하 분포가 어떤 사건을 1회 성공할 때까지 걸리는 시행 횟수에 대한 분포라면, 기하 분포의 합은 음이항 분포로, 사건이 r회 성공할 때까지 걸리는 시행 횟수에 대한 분포입니다.
이런 상생 관계 말이죠! 그중에서 포아송과 감마 분포의 결합은 음이항 분포로 표현이 가능합니다. 포아송 분포와 감마 분포를 결합한다는 건 위에서의 가정처럼 포아송 분포의 모수인 가 감마 분포를 따르도록 만드는 것을 의미합니다.
•
•
라면 이에 대한 marginal 분포는 음이항 분포를 따르게 됩니다.
한 줄 요약하면 위의 BG/NBD 모형의 가정 중 포아송 분포와 감마 분포에 해당하는 부분이 결국 "NBD"에 해당하는 부분입니다. (참조: 링크)
각 분포가 무엇을 의미하길래 왜 이렇게 가정을 했을까? 
위 설명드린 각 분포의 특성은 다음과 같습니다.
•
포아송 분포: 단위 시간 동안의 성공 횟수에 대한 분포
•
감마 분포: 사건을 n번 시행할 때까지의 총 시간에 대한 분포
•
기하 분포: 사건이 1번 발생할 때까지의 시행 횟수에 대한 분포
•
베타 분포: 확률에 대한 분포 (범위: (0,1))
예를 들어 봅시다. 2022년 이후 제 컬리 주문 내역을 보니 총 4번 구매했고, 실제 아래와 같이 구매하였습니다.
날짜 | 구매금액 |
2022.01.16 | 44,159원 |
2022.01.24 | 44,385원 |
2022.02.03 | 40,700원 |
2022.02.05 | 43,520원 |
1.
포아송 분포: 네 달에 거쳐 8번 구매했으니 한 달에 2번 구매한 꼴이 됩니다. 이처럼 한 달의 평균 구매 횟수가 포아송 분포를 따른다 가정합니다.
2.
기하 분포: 여기서의 사건은 “더 이상 구매하지 않는다”라는 것입니다. 더 이상 구매하지 않을 때까지의 총 구매 횟수는 를 따른다 가정합니다.
3.
베타 분포: 마지막으로 이 이탈률 p는 를 따른다 가정합니다.
유저마다 별개의 과거의 구매 정보 RFM (Recency, Frequency, T)을 가지고 위 분포를 따른다 가정하여 가능도 함수를 구해 기댓값을 구하면 유저마다 다른 기대 구매 횟수를 모델링 할 수 있는 것입니다!
Gamma-Gamma 모델
"미래에 유저가 얼마씩 구매할까?"에 대한 모델
BG/NBD 모델은 유저마다 다른 구매 횟수를 모델링 했다면, Gamma-Gamma 모델은 유저별 구매 금액 정보들을 이용합니다.
유저의 일별 구매 금액은 변동이 있죠. 이 변동성을 설명하기 위해 감마 분포를 따른다고 가정합니다. 한 유저가 총 번 구매했다고 할 때, 일별 구매 금액 는 를 따른다 가정합니다. 총 구매 금액은 를 따르고, 평균 구매 금액은 을 따르게 됩니다. 또한 유저들마다 일별 구매 금액이 다르므로, 위 일별 구매 금액이 따르는 감마 분포의 가 또 한 번 를 따른다고 가정합니다.
이 둘의 관계를 갖고 베이즈 정리를 활용한다면 의 사후분포는 를 따르게 됩니다.
그런데 왜 평균 구매 금액에 Gamma 분포를 가정할까?
궁금하지 않습니까? 아까는 감마 분포가 사건이 회 일어날 때까지의 총 시간이라 해놓고 평균 구매 금액 도 감마 분포를 따른다고 할까요?
처음 모델을 개발한 Schmittlein and Peterson (1994)는 건별 구매 금액이 정규 분포를 따른다고 가정했다고 합니다. 그러나 이렇게 가정했을 때의 문제는 정규 분포는 0보다 아래의 값이 나올 수도 있고, 대칭적인 분포라는 점입니다. 돈을 쓰는 행위를 생각해 보면 무조건 구매 금액이 0원보다 많고, 어떤 걸 사느냐에 따라서 가격이 천차만별이기 때문에 대칭적이지 않습니다.
위 예시는 "컬리에서 식재료를 구매" 하는 것이기 때문에 그래도 일관성 있게 4만 원 안팎으로 사긴 하지만, 갑자기 친구들을 초대해서 10만 원을 쓸 수도 있고 가족과 추석을 보내기 위해 20만 원을 쓸 수 있겠죠. 이처럼 구매 금액 자체는 대칭적이기보단 비대칭적이고, 오른쪽으로 치우친 (Right-Skewed) 형태를 띠게 됩니다.
그렇기 때문에 감마 분포가 제격입니다. 0 이상의 값을 가지고, 모수 2개로 비대칭적인 형태를 쉽게 만들 수 있기 때문입니다. 감마 분포가 "시간"의 분포로 쓰일 땐 보통 포아송 분포와 같이 쓰일 때나 그런 것이고, 이 자체로는 0 이상의 범위를 가지고 비대칭적인 분포를 가지는 무언가에 모델링 할 수 있는 좋은 분포인 것입니다.
나가며
지금까지 LTV를 산출하기 위해 기대 구매 횟수와 기대 구매 금액을 모델링 하는 분포들에 대해 살펴보았습니다.
이를 아래와 같이 요약할 수 있습니다.
1. LTV는 기대 구매 횟수 * 기대 구매 금액으로 산출됩니다.
2. 기대 구매 횟수는 BG/NBD 모델을 사용하며, 이는 유저가 향후 구매를 몇 번 할 것인지, 언제 구매를 중단할지를 모델링 합니다.
3. 기대 구매 금액은 Gamma-Gamma 모델을 사용하며 유저가 향후 구매를 얼마나 할 것인지 모델링 합니다.
넥슨 인텔리전스랩스의 플랫폼분석팀에서는 LTV를 비롯해서 다양한 지표를 개발하고 있으며, 플랫폼 단의 분석을 진행하며 의미 있는 인사이트를 찾아내는 것을 목표로 하고 있습니다.
이 글을 읽으면서 지표 개발, 인사이트 발굴에 흥미가 생겼다면, 플랫폼분석팀에서 분석가가 되기 위한 여정에 함께하시길 바랍니다